이동평균선(Moving Average Line, MA)은 특정 기간 동안의 평균 가격을 계산하여 추세를 파악하는데 많이들 참고하고 있습니다.
1. 이동평균선의 종류
1) 단순 이동평균선 (Simple Moving Average, SMA)
- 지정된 기간 동안의 가격(보통 종가)의 산술 평균을 구합니다.
- 예: 5일 SMA는 최근 5일 동안의 종가 합계를 5로 나눈 값.
- 아래 예시 기준으로 10일날의 SMA 가격과 11일날의 SMA 가격 차이는
6일날과 11일 의 종가 가격 차이의 증감분에 비례합니다.

2) 지수 이동평균선(Exponential Moving Average, EMA)
- 최근 가격에 더 큰 가중치를 부여하여, 최신 정보에 더 민감하게 반응하도록 한 이동평균선입니다.
- 트렌드의 변화에 빠르게 반응할 수 있어 단기 분석에 유용합니다.
- 지수 이동평균선 계산 공식
| 1. 초기 EMA 설정 첫 번째 EMA 값은 단순 이동평균(SMA)을 사용하여 계산합니다.  2. 지수 가중치 계산 지수 가중치는 다음과 같이 계산됩니다 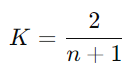 : 지수 가중치 : 이동평균 기간 3. EMA의 반복 계산 초기 값을 계산한 이후 EMA는 다음 식으로 반복적으로 계산됩니다.  : 현재 시점의 EMA : 현재 시점의 가격(보통 종가) : 이전 시점의 EMA : 지수 가중치 |
- 5일 지수이동평균선(EMA)의 예시
| 1. 초기 EMA는 1~5일까지의 종가를 5로 나눈 SMA값입니다. 2. 지수 가중치 K 계산 여기서 n = 5이므로   3. EMA 계산 6일차부터 EMA를 반복적으로 계산  |

3) 가중 이동평균 (Weighted Moving Average, WMA)
- 최근 데이터에 더 큰 가중치를 부여하여 평균값을 계산하는 방식입니다.
- 단순 이동평균(SMA)이나 지수 이동평균(EMA)보다 최신 데이터의 변화에 더 민감하게 반응합니다.
- 가중 이동평균선의 계산법
| 1. 가중치 부여 각 데이터에 일정한 가중치를 부여하며, 가장 최근 데이터에 가장 큰 가중치를 줍니다. 예를 들어, 최근 5일 데이터를 분석할 경우 가중치는 아래와 같이 설정할 수 있습니다: 5일 차 데이터의 가중치: 5 4일 차 데이터의 가중치: 4 3일 차 데이터의 가중치: 3 2일 차 데이터의 가중치: 2 1일 차 데이터의 가중치: 1 2. 가중 평균 계산 공식 WMA는 다음과 같은 공식을 사용합니다.  : 특정 날의 가격(보통 종가) Wi : 해당 날의 가중치 n: 기간 |

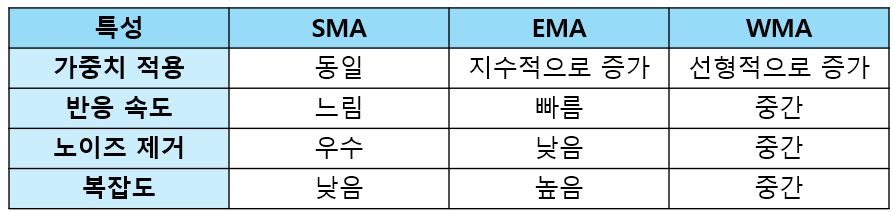
2. 단순이동평균선 vs 지수이동평균선 vs 가중이동평균선
- 일반적으로 종가에 가장 가까운 이평선은 가중 > 지수 > 단순 순서입니다.
- 단순이동평균선(SMA) : 장기적인 추세 확인에 적합
- 지수이동평균선(EMA) : 단기적인 가격 변동에 민감하게 반응하여 빠른 트레이딩에 유용
- 가중이동평균선(WMA) : 최근 데이터에 중점을 두면서도 상대적으로 안정적인 분석이 필요할 때 사용


댓글